What Is K-Fold Cross-Validation?

Yashmeet Singh · May 29, 2022 · 3 minute read

Introduction

We recently covered how to use Train Test Split to train machine learning models.

In this post, we’ll look at Cross-Validation, which builds upon Train Test Split and provides a better estimate of the predictive power of a model.

Train Test Split: A Quick Review

In Train Test Split, we randomly divide a dataset into two subsets. Then we train our model using the training subset. Finally, we evaluate the model’s performance using the test subset.

For example, you could use 75% of the dataset for training and 25% for testing:

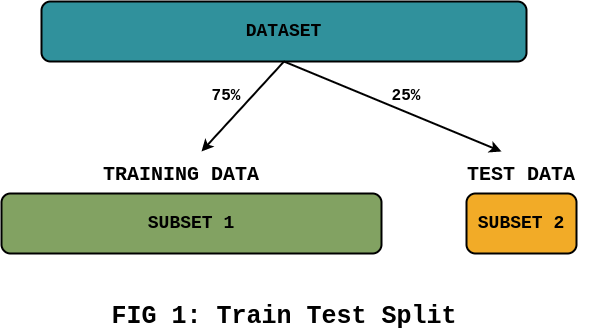
There are a few issues with this approach.

Smaller datasets

If you have a large dataset, using a subset of it to train a model might be acceptable.

However, what if you have a smaller dataset? Splitting such a dataset will leave us with even smaller training and test subsets.

During the training phase, the model may not have enough data to learn the general structure and patterns of the problem at hand. Similarly, using a minuscule subset for testing will provide a poor measure of the model’s performance.

Variable Test Scores

The test dataset must represent the data your model will encounter in the real world.

Since we randomly split the original dataset, we could potentially end up with a test subset that doesn’t represent real-world inputs to our model.

Moreover, every time you execute Train Test Split, the training and test sets could contain different observations than the previous execution. Thus you could get vastly different test scores from one execution to another.

Given these challenges, how do you measure model performance and report the final test score?

Cross-Validation can help alleviate both of these concerns. Let’s explore what it is and how to use it.

Cross-Validation

Cross-Validation works in two steps:

1. Split: Partition the dataset into multiple subsets. We’ll look at a simple splitting strategy (K-Fold).
2. Cross-validate: Create multiple models using combinations of these splits.

Step 1: K-Fold Split

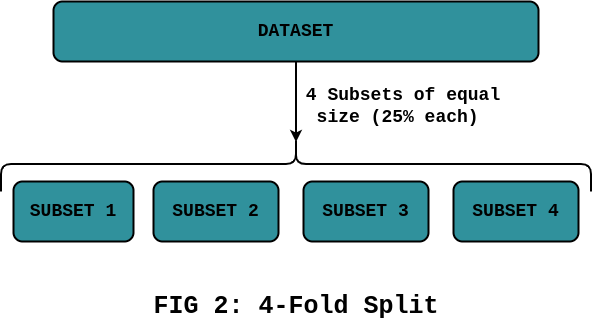
In this step, we split the dataset into a pre-determined number (called ‘K’) of subsets.

For example, if K is 4, we’ll partition the dataset into four subsets at random:

Step 2: K-Fold Cross-Validation

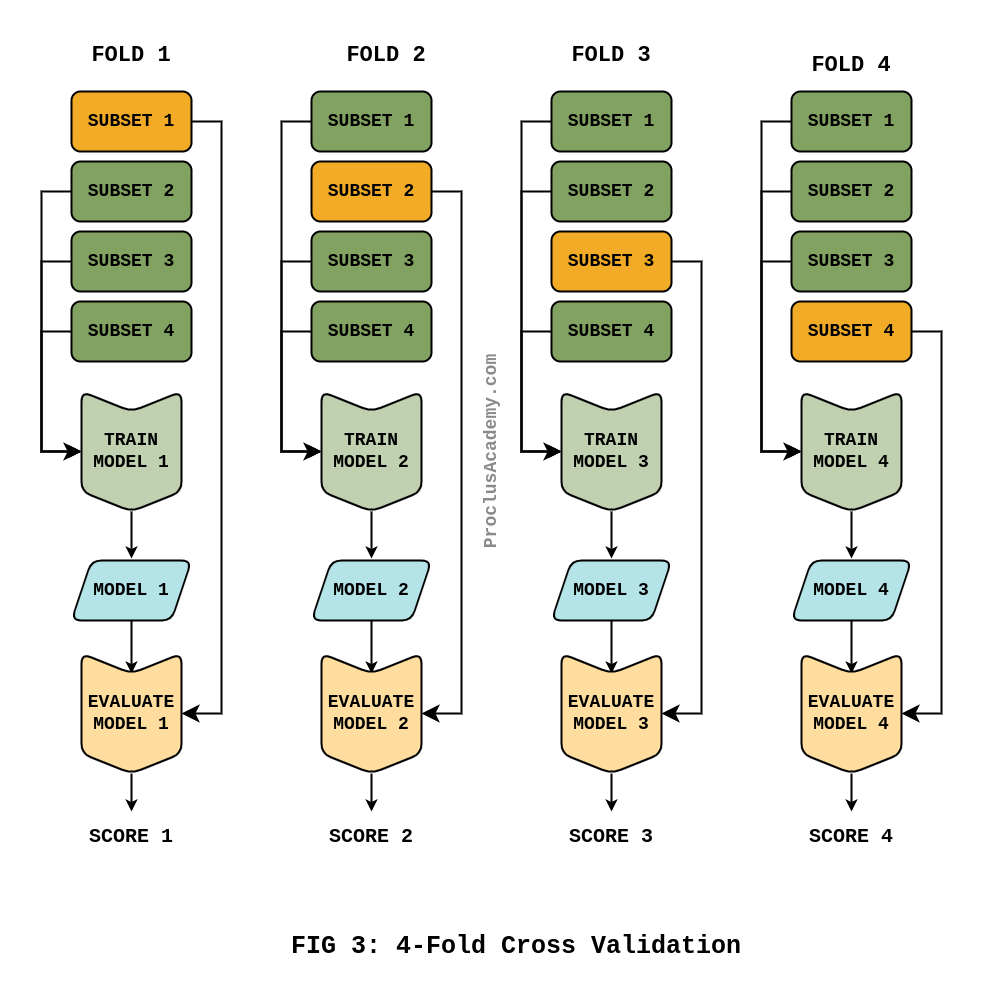
We’ll use one of the K subsets as the test set and train a model using the remaining subsets. For example, train a model using subsets 2, 3, and 4. Then test it using subset 1.

Next, we’ll use another subset as the test set and build a second model using the remaining subsets.

We repeat this process until we have used every subset as a test set. Each iteration of this process is called a fold.

The below diagram shows all the folds using our four subsets:

Reporting Test Scores

K-Fold Cross-Validation will generate multiple test scores. The number of scores equals the number of subsets (K).

How do you report the final test score? You have a few options:

• Mean: Find the average of all the test scores.
• Range: Report the difference between the maximum and minimum test scores.
• Distribution: Calculate the mean and standard deviation of the test scores. It’ll give you a reasonably good idea of the model’s expected performance.
• Any other summary statistics that you may find relevant.

What’s Next?

Now that you know how Cross-Validation works, check out the next article that shows how to implement it using Python and Scikit-Learn library.